SENTIDO NUMÉRICO

Antes de que surgieran los números el hombre se las ingenió para contar, utilizando para ello objetos como piedras, palitos de madera, nudos de cuerdas, o simplemente los dedos. Más adelante comenzaron a aparecer los símbolos gráficos como señales para contar, por ejemplo marcas en una vara o simplemente trazos específicos sobre la arena.
| |
Pero fue en Mesopotamia alrededor del año 4.000 a. C. donde aparecen los primeros vestigios de los números que consistieron en grabados de señales en formas de cuñas sobre pequeños tableros de arcilla empleando para ello un palito aguzado. De aquí el nombre de escritura cuneiforme.
|  |
Este sistema de numeración fue adoptado más tarde, aunque con símbolos gráficos diferentes, por los Griegos y Romanos. Los griegos emplearon simplemente las letras de su alfabeto, mientras que los Romanos además de las letras utilizaron algunos símbolos. En cada actividad humana sea técnica científica o simplemente práctica los números han jugado un papel muy importante... los números siempre están presentes y gobiernan todas las cosas. | |
Aun en las tareas más simples como son la preparación de una comida, hacer compras, medir el tiempo de un juego, comprar el pan, ir a la cantina escolar, colocar los platos y cubiertos sobre la mesa, mirar la talla de la franela que nos gusta para que mamá la compre, en fin, en todas y cada una de las acciones del ser humano se encuentran presente los números. Sería interesante conocer un poco más sobre los números, existen los Números naturales.
| |
Todo número tiene dos valores
Valor por sí mismo: que es siempre el mismo valor esté donde esté colocada cada cifra.
Valor de posición: Es el valor que tiene cada cifra de acuerdo al lugar que ocupa en la cantidad.
Valor de posición: Es el valor que tiene cada cifra de acuerdo al lugar que ocupa en la cantidad.
Observemos la tabla siguiente:
| DECENAS | UNIDADES | |
| 1 | 1 |
Esto me representa el número 111 = Ciento once
Busquemos los valores por sí mismo y el valor de posición del 111
Valor por sí mismo de 111
El valor por sí mismo es el valor que tiene cada número por su figura esté donde esté dentro de la cantidad.
Valor de posición de 111
El valor de posición es el que tiene cada número de acuerdo a donde se encuentre ubicado dentro de la cantidad.

Este lápiz representa 1 UNIDAD por lo tanto dentro de la tabla de posición el número 1 estará dentro de las UNIDADES así:
 Esto quiere decir que tengo 2 UNIDADES
Esto quiere decir que tengo 2 UNIDADES
Por lo tanto coloco el 2 en la casilla de las unidades así:

Busquemos los valores por sí mismo y el valor de posición del 111
Valor por sí mismo de 111
| 1 | = | 1 |
| 1 | = | 1 |
| 1 | = | 1 |
Valor de posición de 111
| 1 Centena |
=
| 100 Unidades |
| 1 Decena |
=
| 10 Unidades |
| 1 Unidad |
=
| 1 Unidad |
El valor de posición es el que tiene cada número de acuerdo a donde se encuentre ubicado dentro de la cantidad.

Este lápiz representa 1 UNIDAD por lo tanto dentro de la tabla de posición el número 1 estará dentro de las UNIDADES así:
| DECENAS | UNIDADES | |
| 1 |

Por lo tanto coloco el 2 en la casilla de las unidades así:
| DECENAS | UNIDADES | |
| 2 |

8 lápices = 8 UNIDADES

Tenemos entonces que buscar con cuántas unidades se forma una DECENA
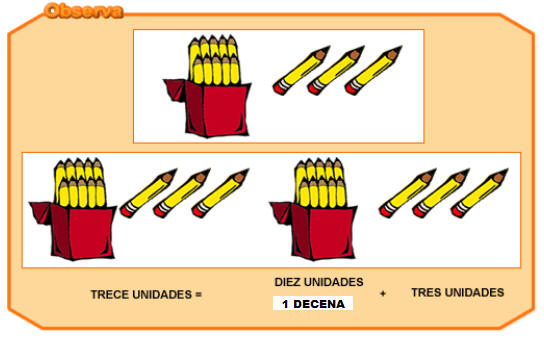
De las 13 UNIDADES que tengo selecciono 10 que me representan 1 DECENA las restantes UNIDADES las coloco en la casilla de las .. UNIDADES
Valor posicional – Forma expandida
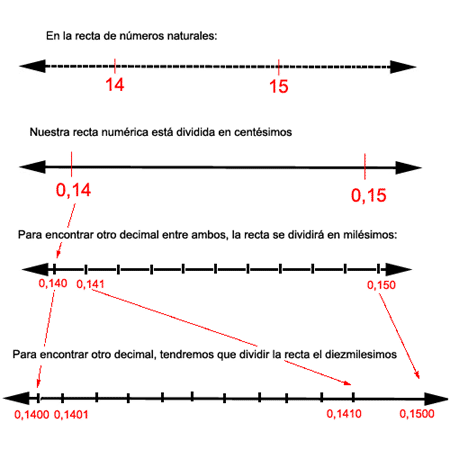
Valores posicionales de los decimales
| DECENAS | UNIDADES | |
| 8 |

¿Cómo colocarías el número 13 dentro de la tabla de posición si cada casilla sólo acepta un número?
De las 13 UNIDADES que tengo selecciono 10 que me representan 1 DECENA las restantes UNIDADES las coloco en la casilla de las .. UNIDADES

Entonces la representación del 13 en la tabla de posiciones quedaría así:
| DECENAS | UNIDADES | |
| 1 | 3 |

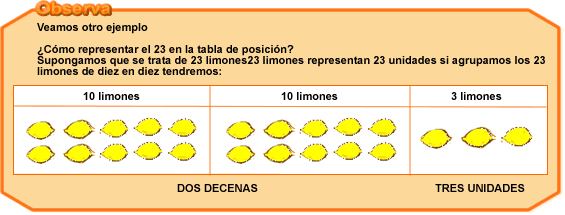
La representación de 23 en la tabla de posición será así:
| DECENAS | UNIDADES | |
| 2 | 3 |
RESUMIENDO
Cuando tu mamá te manda a la panadería a comprar 5 panes, estás comprando 5 UNIDADES de pan.
Pero si en lugar de 5 panes te manda a comprar 34 panes, entonces estás comprando 34 UNIDADES de pan; lo que es lo mismo 3 ...DECENAS de pan (una decena son diez unidades) más 4 UNIDADES de pan.
Cuando tu mamá te manda a la panadería a comprar 5 panes, estás comprando 5 UNIDADES de pan.
Pero si en lugar de 5 panes te manda a comprar 34 panes, entonces estás comprando 34 UNIDADES de pan; lo que es lo mismo 3 ...DECENAS de pan (una decena son diez unidades) más 4 UNIDADES de pan.
Ahora debes estar listo para representar el 34 en la tabla de posición.
| DECENAS | UNIDADES |
Ejercicios
Coloca dentro de la tabla de posición cada una de las cantidades que aparecen a continuación: | DECENAS | UNIDADES | |||
| Así: 394 | 9 | 4 | ||
19
| | |||
450
| ||||
259
|
Valores posicionales

Valor posicional
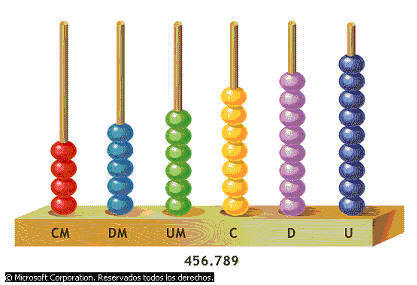
Los números tales como 495,784 tienen seis dígitos. Cada dígito tiene un valor posicional distinto.
El primer dígito se llama centena de mil. Muestra cuantos grupos de cien mil hay en un número. El número 495,784 tiene cuatro centenas de mil.
El segundo dígito es la decena de mil. En este número hay nueve decenas de mil además de las cuatro centenas de mil.
El tercer dígito es la unidad de mil que en este ejemplo es cinco. Por lo tanto hay cuatro grupos de cien mil, nueve grupos de diez mil, y cinco grupo de mil en el número 495,784.
El cuarto dígito se llama centena. Muestra cuantos grupos de mil hay en el número. El número 495,784 tiene siete centenas además de las unidades de mil.
El dígito siguiente corresponde a las decenas. Este número tiene diez decenas además de las cuatro centenas de mil, las nueve decenas de mil, cinco unidades de mil y siete centenas.
El ultimo dígito o dígito de la derecha es el de las unidades que en el ejemplo es cuatro. Por lo tanto hay cuatro grupos de cien mil, nueve grupos de diez mil, cinco grupos de mil, siete grupos de cien, ocho grupos de diez y cuatro unidades en el número 495,784.
Cáda dígito de un número, tal como 495,786, tiene un nombre diferente para cada valor posicional.
En el número 495,786 hay cuatro conjuntos de centanas de mil, 9 conjuntos de decenas de mil, 5 conjuntos de unidades de mil, 7 conjuntos de centenas, 8 conjuntos de decenas y 6 conjuntos de unidades.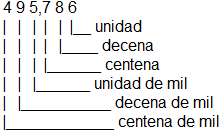
La forma expandida muestra el número en un enunciado de suma. La forma expandida de 495,786 es 400,000 + 90,000 + 5,000 + 700 + 80 + 6.
Valor posicional
Los números tales como 495,784 tienen seis dígitos. Cada dígito tiene un valor posicional distinto.
El primer dígito se llama centena de mil. Muestra cuantos grupos de cien mil hay en un número. El número 495,784 tiene cuatro centenas de mil.
El segundo dígito es la decena de mil. En este número hay nueve decenas de mil además de las cuatro centenas de mil.
El tercer dígito es la unidad de mil que en este ejemplo es cinco. Por lo tanto hay cuatro grupos de cien mil, nueve grupos de diez mil, y cinco grupo de mil en el número 495,784.
El cuarto dígito se llama centena. Muestra cuantos grupos de mil hay en el número. El número 495,784 tiene siete centenas además de las unidades de mil.
El dígito siguiente corresponde a las decenas. Este número tiene diez decenas además de las cuatro centenas de mil, las nueve decenas de mil, cinco unidades de mil y siete centenas.
El ultimo dígito o dígito de la derecha es el de las unidades que en el ejemplo es cuatro. Por lo tanto hay cuatro grupos de cien mil, nueve grupos de diez mil, cinco grupos de mil, siete grupos de cien, ocho grupos de diez y cuatro unidades en el número 495,784.
Valor posicional
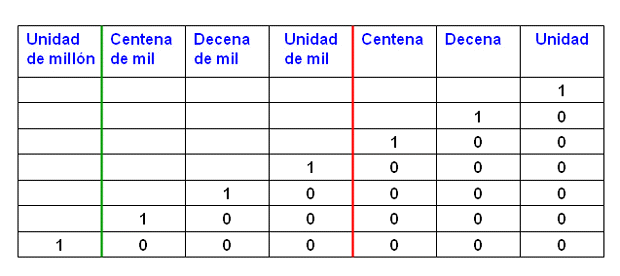
Los números tales como 6,495,784 tienen siete dígitos. Cada digit tiene un valor posicional diferente.
El primer dígito se llama unidad de millón. Hay seis millones en el número 6,495,784.
El Segundo dígito muestra cuantos grupos de centenas de mil hay en el número. El número 6,495, 784 tiene cuatro centenas de mil.
El tercer dígito corresponde a las decenas de mil. Hay nueve decenas de mil además de las seis unidades de millón y las cuatro centenas de mil.
El cuarto dígito corresponde a las unidades de mil que en este ejemplo es cinco.
El quinto dígito es el de las centenas, que es siete en el número 6,495,784.
El dígito siguiente (8) es el lugar correspondiente a las decenas.
El dígito de la derecha o último dígito es el lugar de las unidades que en este ejemplo es cuatro.
Por lo tanto, hay siete grupos de 1,000,000, cuatro grupos de 100,000, nueve grupos de 10,000, cinco grupos de 1000, siete grupos de 100, ocho grupos de 10 y 4 unidades en el número 6,495,784.
Los números decimales tales como 0.6495, tienen cuatro dígitos después del punto decimal. Cada dígito tiene un valor posicional diferente.
El primer dígito después del punto decimal se llama décimo. Hay seis décimos en el número 0.6495.
El segundo dígito indica cuantos centésimos hay en el número. El número 0.6495 tiene cuatro centésimos.
El tercer dígito es el lugar de los milésimos.
El cuarto dígito es el lugar de los diezmilésimos, que en el ejemplo es cinco.
Por lo tanto, hay seis décimos, cuatro centésimos, nueve milésimos, y cinco diezmilésimos en el número 0.6495.
EL VALOR POSICIONAL DE LOS NÚMEROS.

| Los números pueden escribirse de diferentes formas por ejemplo:Ejemplo 1: Forma habitual o más usada: 2, 184, 359, 076 Número en palabras como: Dos billones, ciento ochenta y cuatro millones, trescientos cincuenta y nueve mil, setenta y seis. Forma expandida o desarrollada: 2, 000, 000, 000 + 100, 000, 000 + 80, 000, 000 + 4, 000, 000 + 300, 000 + 50, 000 + 9, 000 + 70 + 6 Ejemplo 2: Forma habitual o más usada: 5.4203 Número en palabras como: cinco y cuatro mil doscientas tres diezmilésima. Forma expandida o desarrollada: 5 + 0.4 + 0.02 + 0.0003 PRACTICA: Completa la siguiente tabla:
COMPARA Y ORDENA NÚMEROS CARDINALES
Los números se ordenan comparando los dígitos que estén en la misma posición por ejemplo:
Si comparamos las siguientes cantidades:
• 54, 253,400 y 68, 883,000 ambas tienen los mismos dígitos y el valor de posición mayor corresponde a la decena de millón. Los primeros dígitos que corresponde a la decena de millón son el 5 y el 6, siendo el 6 mayor que el 5 por lo que 68, 883,000 es mayor que 54, 253,400
• 39, 125,200 y 38, 120,000 tienen también los mismos dígitos, el valor de posición mayor corresponde también a la decena de millón , siendo ambas cantidades iguales a 3, por lo que comparamos los siguientes dígitos como 9 es mayor que 8 entonces 39, 125,200 es mayor que 38, 120,00.
• 5, 200,033 y 225,032 en este caso las cantidades no tienen los mismos dígitos, siendo la que tiene más dígitos la mayor, entonces 5, 200,033 es mayor que 225,032
RECUERDEN QUE:
> significa mayor que 39, 125,200 > 38, 120,00.
< significa menor que 54, 253,400 < 68, 883,000
PRACTICA
1-Compara los números de cada par:
• 223, 125,143____ 325, 100,300
• 5, 256,200_____ 15, 457,010
• 197,405____ 97,400
2-Ordena en forma ascendente: (menor a mayor)
540, 120,033 744, 130,000 74, 130,001 604,200 544, 105,000
______________< _______________< ________________< _______________< __________________
3-Ordena en forma descendente: (mayor a menor)
55, 753,506 232, 608,000 99, 105,070 123,304 205, 190,002
_______________> _______________> ________________ > _______________> _______________
COMPARA Y ORDENA NÚMEROS DECIMALES

Los números decimales se comparan primeramente comparando la parte entera y si la misma es igual se comparan las partes decimales.
Si comparamos las siguientes cantidades:
•13.40 12.50 12.59 12.64:
13>12 el número mayor es el que tiene la parte entera mayor por lo que
13.40 > 12.64
De los restantes números el mayor será el que tiene el dígito de las décimas mayor
12.64 y 12.59 como 6 > 5 entonces 12.64 >12.59
Nos quedarían comparar el 12.59 con el 12.50 en este caso el número mayor es el que tiene el digito de las centésimas mayor. Entonces 12.59 > 12.50
Ordenando los números en orden ascendente (de menor a mayor) tendríamos:
12.50 < 12.59 < 12.64 < 13.40
PRACTICA
1- Compara los números de cada par utiliza los signos <, o >:
• 12.10___ 11.20
• 12.23___12.34
• 12.25___ 12.23
2- Ordena de forma ascendente: (menor a mayor)
4.025 4.611 4.007 4.614 4.1094
_____________> ______________ >_______________ >______________ > ______________
3- Ordena en forma descendente: (mayor a menor)
5.4321 5.0007 5.4734 5.103 6.0021
_____________< _______________ < ______________ < ______________ < ______________
REDONDEA NÚMEROS CARDINALES
Usamos el redondeo cuando queremos aproximar una cantidad a uno de sus dígitos en específico.
Ejemplo: Si en un almacén hay 27,190 lápices rojos y 22,180 lápices azules para ser distribuidos a las escuelas de la zona si queremos conocer el número aproximado de lápices redondeando al último dígito:
Lápices rojos
• 27,190 Se localiza el ultimo dígito en este caso es la decena de millar o de mil.
• 27,190 Se observa el dígito que está a su derecha, si el número es menor que 5, el número que está en la posición que se va a redondear se deja igual y el resto de dígitos se cambian por cero. Si el digito es mayor que 5, se suma 1 al que se va a redondear y el resto de los dígitos a la derecha se cambian por ceros.
• 30,000 En nuestro caso 7 es mayor que 5.
Lápices azules
• 22,180 Ultimo dígito.
• 22,180 Observamos el dígito que está a su derecha y es menor que 5, por lo que el número que está en la posición que se va a redondear se deja igual.
• 22,000 En nuestro caso 2 es menor que 5
PRACTICA:
1) Redondea 223,105 a:
• A la decena de mil o millar más cercana_________________________________.
• A la unidad de mil o millar más cercana__________________________________.
• A la centena más cercana_____________________________________________.
2) Redondea 11,305, 506 a:
• A la unidad de millón más cercana______________________________________.
• A la centena de mil o millar más cercana_________________________________.
• A la decena de mil o millar más cercana_________________________________.
• A la unidad de mil o millar más cercana_________________________________.
• A la centena más cercana_____________________________________________.
ORDEN DE OPERACIONES BÁSICAS Están establecidas reglas para resolver las expresiones matemáticas donde se necesiten realizar varias operaciones básicas, que se denominan Orden de Operaciones y son las siguientes: • Se resuelve la o las operaciones que aparezcan entre paréntesis • Se multiplica o divide de izquierda a derecha. → • Se suma o resta de izquierda a derecha. → Analizando los siguientes ejemplos tenemos: 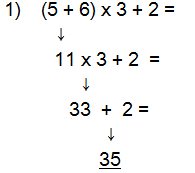 Por tanto (5 + 6) x 3 + 2 = 35 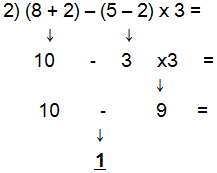 Por tanto (8 + 2) – (5 – 2) x 3 = 1 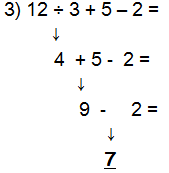 Por tanto 12 ÷ 3 + 5 – 2 = 7
LAS POTENCIAS Y SUS EXPONENTES
Usamos los exponentes para representar la multiplicación de dos factores o más de igual valor

forma exponencial factores forma común o usual
Se lee tres al cuadrado o tres elevado a la segunda potencia.
Ejemplos:
1) 4 x 4 x 4 x 4 x 4 = 1024 ó 45 = 1024
Se lee cuatro elevado a la quinta potencia.
2) 5 x 5 x 5 = 125 ó 53 = 125
Se lee cinco elevado al cubo o cinco elevado a la tercera potencia.
20 = 1 Cualquier número elevado a la potencia 0 es igual a 1, 40 = 1
PRACTICA
1) Convierte cada expresión aritmética en una expresión exponencial:
• 2 x 2 x 2 x 2 x 2 x 2 x 2 = _____ • 100 x 100 x 100=_____
• 6 x 6 = _____ • 10 x 10 x 10 x 10 = ____
2) Escribe los factores de cada forma exponencial:
• 72 =_______________________
• 86 =_______________________
• 91 =_______________________
3) Escribe cada número en forma común o usual:
• 54=_______ • 33=_________
• 45=_______ • 28=_________
REDONDEO DE NÚMEROS DECIMALES
Cuando redondeamos números decimales, lo hacemos aproximando la parte decimal.
Ejemplo:
1) Queremos redondear el número 32. 243 a la decima más cercana:
• 32.243 Se marca el dígito que se vaya a redondear en este caso la decima.
• 32.243 Se observa el dígito que está a su derecha en este caso en la posición de las centésimas en este caso es el dígito 4 que es menor que 5 4< 5.
• 32.2 Como el dígito de la centésima es menor que 5 se queda igual y se eliminan el resto de los dígitos.
2) Queremos redondear el número 54. 671 a la decima más cercana:
• 54. 671 Se marca el dígito que se vaya a redondear en este caso la decima.
• 54.671 Se observa el dígito que está a su derecha en este caso en la posición de las
centésimas en este caso es el dígito 7 que es mayor que 5 7>5.
• 54.7 Como el dígito de la centésima es igual o mayor que 5, se suma 1 a la decima 6+ 1
y se eliminan el resto de los dígitos.
3) Queremos redondear el número 2.0368 a la milésima más cercana:
• 2.0368 Se marca el dígito que se vaya a redondear en este caso la milésima.
• 2.0368 Se observa el dígito que está a su derecha en este caso en la posición de las
diezmilésimas el dígito 8 es mayor que 5 8>5.
• 2.037 Como el dígito de la diezmilésima es mayor que 5, se suma 1 a la milésima
PRACTICA
1) Redondea 2.3457
• A la decima más cercana_____________________________.
• A la centésima más cercana__________________________.
• A la milésima más cercana___________________________.
2) Redondea 2.3457
• A la decima más cercana_____________________________.
• A la centésima más cercana__________________________.
• A la milésima más cercana___________________________.
 |
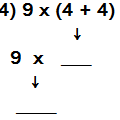



 2 Dm + 5 Um + 3 CM + 0 DM + 1 UM + 4 C + 5 D + 8 U
2 Dm + 5 Um + 3 CM + 0 DM + 1 UM + 4 C + 5 D + 8 U